小学校3年生の「あまりのあるわり算」の授業
今回は「割り切れない場合の除法について理解し、除法の意味について理解を深めるとともに、それを用いることができるようにする」ことを目標とした授業実践のレポートである。
単元全体にわたる教材研究の結果から、大事にしたことは、以下の5点である。
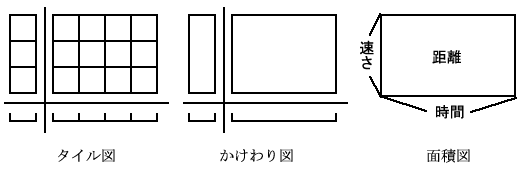
- かけわり図を活用し、演算決定に役立てる。
- かけわり図の導入にあたっては、かけわりマシーンを使い、具体的な操作をしながら指導していく。
- 式には名数をつける
- 式には、/(パー)もつけ、1あたりの量、いくつ分、全体量を意識させる。
- 文章題の答えは、文章で書かせることで、何を求めているのか常に意識させる。
かけわり図の一例
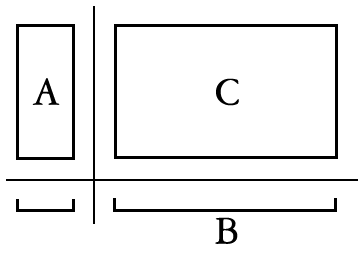
上図で、Aは「1あたりの量」、Bは「いくつ分」、Cは「全体量」を表していて、
Cを求めること:掛け算
Aを求めること:割り算(等分除)
Bを求めること:割り算(包含除)
となって、乗法・除法を1つの図で表現でき、この図を用いることによって、演算決定をスムーズに行なうことができる。
かけわり図は、2年生の掛け算で用いるタイル図の自然な延長であり、さらに高学年での面積図へと発展していく。
『かけわりマシーン』の使用方法
【問題】チョコレートが14個あります。1人に3個ずつ分けます。何人に分けられますか?
この問題を前述した「かけわり図」に当てはめると、Aが3個、Cが14個であり、求めるものがBであることを確認することができる。
そして、立式は「14個÷3個/人=?人」となる。
答えを求める段階になって、子どもたちの顔に困惑の表情が生じる。
なぜなら、あまりが出てきて、きちんと分けられないからである。
本時の授業以前では、必ず、きちんと分けられる場合ばかりであったから、あまりが出てくる場合、どのように処理してよいのか戸惑うわけである。
そこで登場するのが、下の写真のような『かけわりマシーン』である。
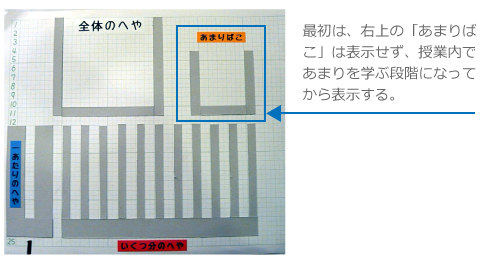
【手順】
- 「全体のへや」にチョコレートを14個置く。
- 「1あたりのへや」が3個であることから、「いくつ分のへや」のそれぞれに3個ずつ入れていく。
すると、3個ずつ4人に分けることができるが、2個のあまりが出てきてしまう。
この2個をどのように処理すればよいかが議論になる。
議論は「あまりばこ」を作り、そこへあまった2個を置いておくことで決着がつく。
わざわざ「あまりばこ」を作らなくても、もとの「全体のへや」に置いておけばよいではないかという意見もあるが、それでは分けたことにならないというのが子どもの気持ちである。
教具や絵・図を使用する重要性
算数の授業において、教具や絵・図を使用することは理解を深める上できわめて重要であり、かけわり図を使うことは、3年生の子どもたちにとって、理解しやすく有効であることが改めてわかった。
『かけわりマシーン』は、具体物の操作からかけわり図につなげていくのにわかりやすいツールであり、子どもたちにわり算のイメージをつけやすく、意欲的に取り組むことができるといえる。
